BASIC ELECTRONICS full course : Voltage, Current, Batteries, Circuit Elements,power,capacitor and JFET

Basic Electronics   

    

The goal of this chapter is to provide some basic information about electronic circuits. We make the assumption that you have no prior knowledge of electronics, electricity, or circuits, and start from the basics. This is an unconventional approach, so it may be interesting, or at least amusing, even if you do have some experience. So, the first question is ``What is an electronic circuit?'' A circuit is a structure that directs and controls electric currents, presumably to perform some useful function. The very name "circuit" implies that the structure is closed, something like a loop. That is all very well, but this answer immediately raises a new question: "What is an electric current?" Again, the name "current" indicates that it refers to some type of flow, and in this case we mean a flow of electric charge, which is usually just called charge because electric charge is really the only kind there is. Finally we come to the basic question:

What is Charge?

 

No one knows what charge really is anymore than anyone knows what gravity is. Both are models, constructions, fabrications if you like, to describe and represent something that can be measured in the real world, specifically a force. Gravity is the name for a force between masses that we can feel and measure. Early workers observed that bodies in "certain electrical condition" also exerted forces on one another that they could measure, and they invented charge to explain their observations. Amazingly, only three simple postulates or assumptions, plus some experimental observations, are necessary to explain all electrical phenomena. Everything: currents, electronics, radio waves, and light. Not many things are so simple, so it is worth stating the three postulates clearly.

Charge exists.   

We just invent the name to represent the source of the physical force that can be observed. The assumption is that the more charge something has, the more force will be exerted. Charge is measured in units of Coulombs, abbreviated C. The unit was named to honor Charles Augustin Coulomb (1736-1806) the French aristocrat and engineer who first measured the force between charged objects using a sensitive torsion balance he invented. Coulomb lived in a time of political unrest and new ideas, the age of Voltaire and Rousseau. Fortunately, Coulomb completed most of his work before the revolution and prudently left Paris with the storming of the Bastille.

Charge comes in two styles.

We call the two styles positive charge, $+$, and (you guessed it) negative charge, $-$. Charge also comes in lumps of $1.6\; �10$^-19C , which is about two ten-million-trillionths of a Coulomb. The  discrete nature of charge is not important for this discussion, but it does serve to indicate that a Coulomb is a LOT of charge.

Charge is conserved.

You cannot create it and you cannot annihilate it. You can, however, neutralize it. Early workers observed experimentally that if they took equal amounts of positive and negative charge and combined them on some object, then that object neither exerted nor responded to electrical forces; effectively it had zero net charge. This experiment suggests that it might be possible to take uncharged, or neutral, material and to separate somehow the latent positive and negative charges. If you have ever rubbed a balloon on wool to make it stick to the wall, you have separated charges using mechanical action.

Those are the three postulates. Now we will present some of the experimental findings that both led to them and amplify their significance.

 

Voltage   

 

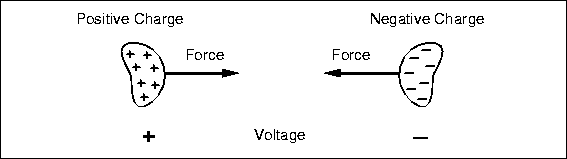
First we return to the basic assumption that forces are the result of charges. Specifically, bodies with opposite charges attract, they exert a force on each other pulling them together. The magnitude of the force is proportional to the product of the charge on each mass. This is just like gravity, where we use the term "mass" to represent the quality of bodies that results in the attractive force that pulls them together (see Fig. 4.1).

  

Figure 4.1: Opposite charges exert an attractive force on each other, just like two masses attract. External force is required to hold them apart, and work is required to move them farther apart.

Electrical force, like gravity, also depends inversely on the distance squared between the two bodies; short separation means big forces. Thus it takes an opposing force to keep two charges of opposite sign apart, just like it takes force to keep an apple from falling to earth. It also takes work and the expenditure of energy to pull positive and negative charges apart, just like it takes work to raise a big mass against gravity, or to stretch a spring. This stored or potential energy can be recovered and put to work to do some useful task. A falling mass can raise a bucket of water; a retracting spring can pull a door shut or run a clock. It requires some imagination to devise ways one might hook on to charges of opposite sign to get some useful work done, but it should be possible.

The potential that separated opposite charges have for doing work if they are released to fly together is called voltage, measured in units of volts (V). (Sadly, the unit volt is not named for Voltaire, but rather for Volta, an Italian scientist.) The greater the amount of charge and the greater the physical separation, the greater the voltage or stored energy. The greater the voltage, the greater the force that is driving the charges together. Voltage is always measured between two points, in this case, the positive and negative charges. If you want to compare the voltage of several charged bodies, the relative force driving the various charges, it makes sense to keep one point constant for the measurements. Traditionally, that common point is called "ground."

Early workers, like Coulomb, also observed that two bodies with charges of the same type, either both positive or both negative, repelled each other (Fig. 4.2). They experience a force pushing

  

Figure 4.2: Like charges exert a repulsive force on each other. External force is required to hold them together, and work is required to push them closer.

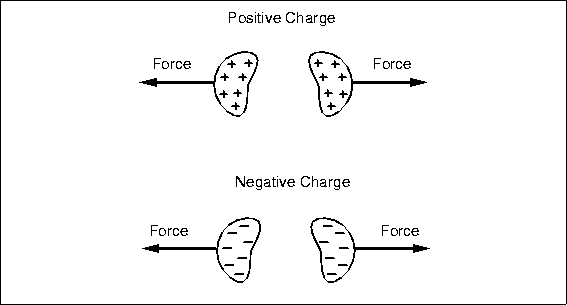them apart, and an opposing force is necessary to hold them together, like holding a compressed spring. Work can potentially be done by letting the charges fly apart, just like releasing the spring. Our analogy with gravity must end here: no one has observed negative mass, negative gravity, or uncharged bodies flying apart unaided. Too bad, it would be a great way to launch a space probe. The voltage between two separated like charges is negative; they have already done their work by running apart, and it will take external energy and work to force them back together.

So how do you tell if a particular bunch of charge is positive or negative? You can't in isolation. Even with two charges, you can only tell if they are the same (they repel) or opposite (they attract). The names are relative; someone has to define which one is "positive." Similarly, the voltage between two points $A$ and $B$, $V$_AB , is relative. If $V$_AB is positive you know the two points are oppositely charged, but you cannot tell if point $A$ has positive charge and point $B$ negative, or visa versa. However, if you make a second measurement between $A$ and another point $C$, you can at least tell if $B$ and $C$ have the same charge by the relative sign of the two voltages, $V$_AB and $V$_AC to your common point $A$. You can even determine the voltage between $B$ and $C$ without measuring it: $V$_BC = V_AC - V_AB . This is the advantage of defining a common point, like $A$, as ground and making all voltage measurements with respect to it. If one further defines the charge at point $A$ to be negative charge, then a positive $V$_AB means point $B$ is positively charged, by definition. The names and the signs are all relative, and sometimes confusing if one forgets what the reference or ground point is.

 

Current   

Charge is mobile and can flow freely in certain materials, called conductors. Metals and a few other elements and compounds are conductors. Materials that charge cannot flow through are called insulators. Air, glass, most plastics, and rubber are insulators, for example. And then there are some materials called semiconductors, that, historically, seemed to be good conductors sometimes but much less so other times. Silicon and germanium are two such materials. Today, we know that the difference in electrical behavior of different samples of these materials is due to extremely small amounts of impurities of different kinds, which could not be measured earlier. This recognition, and the ability to precisely control the "impurities" has led to the massive semiconductor electronics industry and the near-magical devices it produces, including those on your RoboBoard. We will discuss semiconductor devices later; now let us return to conductors and charges.

Imagine two oppositely charged bodies, say metal spheres, that are being held apart, as in Fig. 4.3.

  

Figure 4.3: Two spheres with opposite charges are connected by a conductor, allowing charge to flow.

There is a force between them, the potential for work, and thus a voltage. Now we connect a conductor between them, a metal wire. On the positively charged sphere, positive charges rush along the wire to the other sphere, repelled by the nearby similar charges and attracted to the distant opposite charges. The same thing occurs on the other sphere and negative charge flows out on the wire. Positive and negative charges combine to neutralize each other, and the flow continues until there are no charge differences between any points of the entire connected system. There may be a net residual charge if the amounts of original positive and negative charge were not equal, but that charge will be distributed evenly so all the forces are balanced. If they were not, more charge would flow. The charge flow is driven by voltage or potential differences. After things have quieted down, there is no voltage difference between any two points of the system and no potential for work. All the work has been done by the moving charges heating up the wire.

The flow of charge is called electrical current. Current is measured in amperes (a), amps for short (named after another French scientist who worked mostly with magnetic effects). An ampere is defined as a flow of one Coulomb of charge in one second past some point. While a Coulomb is a lot of charge to have in one place, an ampere is a common amount of current; about one ampere flows through a 100 watt incandescent light bulb, and a stove burner or a large motor would require ten or more amperes. On the other hand low power digital circuits use only a fraction of an ampere, and so we often use units of $1/1000$ of an ampere, a milliamp, abbreviated as ma, and even $1/1000$ of a milliamp, or a microamp, $�a$. The currents on the RoboBoard are generally in the milliamp range, except for the motors, which can require a full ampere under heavy load. Current has a direction, and we define a positive current from point $A$ to $B$ as the flow of positive charges in the same direction. Negative charges can flow as well, in fact, most current is actually the result of negative charges moving. Negative charges flowing from $A$ to $B$ would be a negative current, but, and here is the tricky part, negative charges flowing from $B$ to $A$ would represent a positive current from $A$ to $B$. The net effect is the same: positive charges flowing to neutralize negative charge or negative charges flowing to neutralize positive charge; in both cases the voltage is reduced and by the same amount.

Batteries   

Charges can be separated by several means to produce a voltage. A battery uses a chemical reaction to produce energy and separate opposite sign charges onto its two terminals. As the charge is drawn off by an external circuit, doing work and finally returning to the opposite terminal, more chemicals in the battery react to restore the charge difference and the voltage. The particular type of chemical reaction used determines the voltage of the battery, but for most commercial batteries the voltage is about 1.5 V per chemical section or cell. Batteries with higher voltages really contain multiple cells inside connected together in series. Now you know why there are 3 V, 6 V, 9 V, and 12 V batteries, but no 4 or 7 V batteries. The current a battery can supply depends on the speed of the chemical reaction supplying charge, which in turn often depends on the physical size of the cell and the surface area of the electrodes. The size of a battery also limits the amount of chemical reactants stored. During use, the chemical reactants are depleted and eventually the voltage drops and the current stops. Even with no current flow, the chemical reaction proceeds at a very slow rate (and there is some internal current flow), so a battery has a finite storage or shelf life, about a year or two in most cases. In some types of batteries, like the ones we use for the robot, the chemical reaction is reversible: applying an external voltage and forcing a current through the battery, which requires work, reverses the chemical reaction and restores most, but not all, the chemical reactants. This cycle can be repeated many times. Batteries are specified in terms of their terminal voltage, the maximum current they can deliver, and the total current capacity in ampere-hours.

You should handle batteries carefully, especially the ones we use in this course. Chemicals are a very efficient and compact way of storing energy. Just consider the power of gasoline or explosives, or the fact that you can play soccer for several hours powered only by a slice of cold pizza for breakfast. Never connect the terminals of a battery together with a wire or other good conductor. The battery we use for the RoboBoard is similar to the battery in cars, which uses lead and sulphuric acid as reactants. Such batteries can deliver very large currents through a short circuit, hundreds of  amperes. The large current will heat the wire and possibly burn you; the resulting rapid internal chemical reactions also produce heat and the battery can explode, spreading nasty, reactive chemicals about. Charging these batteries with too large a current can have the same effect. Double check the circuit and instructions before connecting a battery to any circuit. More information on batteries can be found in Chapter 7.

Circuit Elements

Resistors   

  

We need some way to control the flow of current from a voltage source, like a battery, so we do not melt wires and blow up batteries. If you think of current, charge flow, in terms of water flow, a good electrical conductor is like big water pipe. Water mains and fire hoses have their uses, but you do not want to take a drink from one. Rather, we use small pipes, valves, and other devices to limit water flow to practical levels. Resistors do the same for current; they resist the flow of charge; they are poor conductors. The value of a resistor is measured in ohms and represented by the Greek letter capital omega. There are many different ways to make a resistor. Some are just a coil of wire made of a material that is a poor conductor. The most common and inexpensive type is made from powdered carbon and a glue-like binder. Such carbon composition resistors usually have a brown cylindrical body with a wire lead on each end, and colored bands that indicate the value of the resistor. The key to reading these values is given in Chapter 2.

There are other types of resistors in your robot kit. The potentiometer is a variable resistor. When the knob of a potentiometer is turned, a slider moves along the resistance element. Potentiometers generally have three terminals, a common slider terminal, and one that exhibits increasing resistance and one that has decreasing resistance relative to the slider as the  shaft is turned in one direction. The resistance between the two stationary contacts is, of course, fixed, and is the value specified for the potentiometer. The photoresistor or photocell is composed of a light sensitive material. When the photocell is exposed to more light, the resistance decreases. This type of resistor makes an excellent light sensor.

&nbsp

Ohm's Law

Ohm's law describes the relationship between voltage, $V$, which is trying to force charge to flow, resistance, $R$, which is resisting that flow, and the actual resulting current $I$. The relationship is simple and very basic: .   Thus large voltages and/or low resistances produce large currents. Large resistors limit current to low values. Almost every circuit is more complicated than just a battery and a resistor, so which voltage does the formula refer to? It refers to the voltage across the resistor, the voltage between the two terminal wires. Looked at another way, that voltage is actually produced by the resistor. The resistor is restricting the flow of charge, slowing it down, and this creates a traffic jam on one side, forming an excess of charge with respect to the other side. Any such charge difference or separation results in a voltage between the two points, as explained above. Ohm's law tells us how to calculate that voltage if we know the resistor value and the current flow. This voltage drop is analogous to the drop in water pressure through a small pipe or small nozzle.

 

Power   

Current flowing through a poor conductor produces heat by an effect similar to mechanical friction. That heat represents energy that comes from the charge traveling across the voltage difference. Remember that separated charges have the potential to do work and provide energy. The work involved in heating a resistor is not very useful, unless we are making a hotplate; rather it is a byproduct of restricting the current flow. Power is measured in units of watts (W), named after James Watt, the Englishman who invented the steam engine, a device for producing lots of useful power. The power that is released into the resistor as heat can be calculated as $P=VI$, where $I$ is the current flowing through the resistor and $V$ is the voltage across it. Ohm's law relates these two quantities, so we can also calculate the power as The power produced in a resistor raises its temperature and can change its value or destroy it. Most resistors are air-cooled and they are made with different power handling capacity. The most common values are 1/8, 1/4, 1, and 2 watt resistors, and the bigger the wattage rating, the bigger the resistor physically. Some high power applications use special water cooled resistors. Most of the resistors on the RoboBoard are 1/8 watt.

Combinations of Resistors   

 

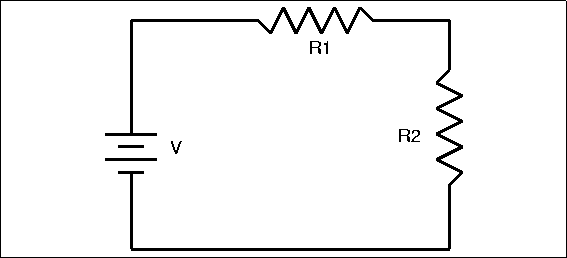
Resistors are often connected together in a circuit, so it is necessary to know how to determine the resistance of a combination of two or more resistors. There are two basic ways in which resistors can be connected: in series and in parallel. A simple series resistance circuit is shown in Figure 4.4.

  

Figure 4.4: Two Resistors in Series

Determining the total resistance for two or more resistors in series is very simple. Total resistance equals the sum of the individual resistances. In this case, $R$_T=R₁+R2 . This makes common sense; if you think again in terms of water flow, a series of obstructions in a pipe add up to slow the flow more than any one. The resistance of a series combination is always greater than any of the individual resistors.

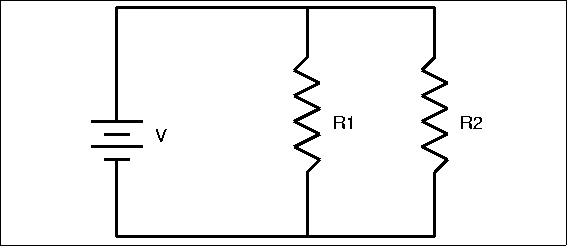
The other method of connecting resistors is shown in Figure 4.5, which shows a simple parallel resistance circuit.

  

Figure 4.5: Two Resistors in Parallel

Our water pipe analogy indicates that it should be easier for current to flow through this multiplicity of paths, even easier than it would be to flow through any single path. Thus, we expect a parallel combination of resistors to have less resistance than any one of the resistors. Some of the total current will flow through R1 and some will flow through R2, causing an equal voltage drop across each resistor. More current, however, will flow through the path of least resistance. The formula for total resistance in a parallel circuit is more complex than for a series circuit:

$R$T={1{1R1}+{1R2}...+{1Rn}}

(1)

Parallel and series circuits can be combined to make more complex structures, but the resulting complex resistor circuits can be broken down and analyzed in terms of simple series or parallel circuits. Why would you want to use such combinations? There are several reasons; you might use a combination to get a value of resistance that you needed but did not have in a single resistor. Resistors have a maximum voltage rating, so a series of resistors might be used across a high voltage. Also, several low power resistors can be combined to handle higher power. What type of connection would you use?

Capacitors   

  

Capacitors are another element used to control the flow of charge in a circuit. The name derives from their capacity to store charge, rather like a small battery. Capacitors consist of two conducting surfaces separated by an insulator; a wire lead is connected to each surface. You can imagine a capacitor as two large metal plates separated by air, although in reality they usually consist of thin metal foils or films separated by plastic film or another solid insulator, and rolled up in a compact package. 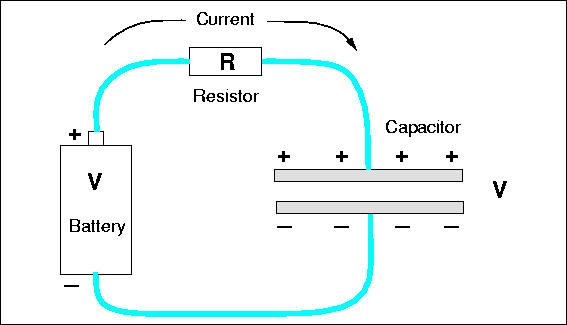Consider connecting a capacitor across a battery, as in Fig. 4.6.

  

Figure 4.6: A simple capacitor connected to a battery through a resistor.

As soon as the connection is made charge flows from the battery terminals, along the wire and onto the plates, positive charge on one plate, negative charge on the other. Why? The like-sign charges on each terminal want to get away from each other. In addition to that repulsion, there is an attraction to the opposite-sign charge on the other nearby plate. Initially the current is large, because in a sense the charges can not tell immediately that the wire does not really go anywhere, that there is no complete circuit of wire. The initial current is limited by the resistance of the wires, or perhaps by a real resistor, as we have shown in Fig. 4.6. But as charge builds up on the plates, charge repulsion resists the flow of more charge and the current is reduced. Eventually, the repulsive force from charge on the plate is strong enough to balance the force from charge on the battery terminal, and all current stops. Figure 4.7 shows how the current might vary with

  

Figure 4.7: The time dependence of the current in the circuit of Fig. 4.6 for two values of resistance.

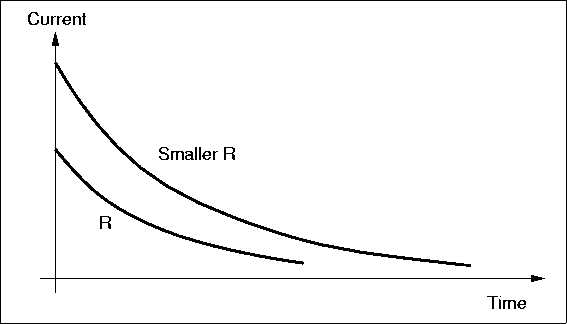time for two different values of resistors. For a large resistor, the whole process is slowed because the current is less, but in the end, the same amount of charge must exist on the capacitor plates in both cases. The magnitude of the charge on each plate is equal.

The existence of the separated charges on the plates means there must be a voltage between the plates, and this voltage be equal to the battery voltage when all current stops. After all, since the points are connected by conductors, they should have the same voltage; even if there is a resistor in the circuit, there is no voltage across the resistor if the current is zero, according to Ohm's law. The amount of charge that collects on the plates to produce the voltage is a measure of the value of the capacitor, its capacitance, measured in farads (f). The relationship is $C\; =\; Q/V$, where Q is the charge in Coulombs. Large capacitors have plates with a large area to hold lots of charge, separated by a small distance, which implies a small voltage. A one farad capacitor is extremely large, and generally we deal with microfarads ($�f$), one millionth of a farad, or picofarads (pf), one trillionth $(10$^-12) of a farad.

Consider the   circuit of Fig. 4.6 again. Suppose we cut the wires after all current has stopped flowing. The charge on the plates is now trapped, so there is still a voltage between the terminal wires. The charged capacitor looks somewhat like a battery now. If we connected a resistor across it, current would flow as the positive and negative charges raced to neutralize each other. Unlike a battery, there is no mechanism to replace the charge on the plates removed by the current, so the voltage drops, the current drops, and finally there is no net charge left and no voltage differences anywhere in the circuit. The behavior in time of the current, the charge on the plates, and the voltage looks just like the graph in Fig. 4.7. This curve is an exponential function: $exp(-t/RC)$. The voltage, current, and charge fall to about 37% of their starting values in a time of $R\; �C$ seconds, which is called the characteristic time or the time constant of the circuit. The $RC$ time constant is a measure of how fast the circuit can respond to changes in conditions, such as attaching the battery across the uncharged capacitor or attaching a resistor across the charged capacitor. The voltage across a capacitor cannot change immediately; it takes time for the charge to flow, especially if a large resistor is opposing that flow. Thus, capacitors are used in a circuit to damp out rapid changes of voltage.

Combinations of Capacitors   

Like resistors, capacitors can be joined together in two basic ways: parallel and series. It should be obvious from the physical construction of capacitors that connecting two together in parallel results in a bigger capacitance value. A parallel connection results in bigger capacitor plate area, which means they can hold more charge for the same voltage. Thus, the formula for total capacitance in a parallel circuit is:

$C$T=C1+C2...+Cn ,

(2)

the same form of equation for resistors in series, which can be confusing unless you think about the physics of what is happening.

The capacitance of a series connection is lower than any capacitor because for a given voltage across the entire group, there will be less charge on each plate. The total capacitance in a series circuit is

$C$T={1{1C1}+{1C2}...+{1Cn}}.

(3)

Again, this is easy to confuse with the formula for parallel resistors, but there is a nice symmetry here.

 

Inductors   

Inductors are the third and final type of basic circuit component. An inductor is a coil of wire with many windings, often wound around a core made of a magnetic material, like iron. The properties of inductors derive from a different type of force than the one we invented charge to explain: magnetic force rather than electric force. When current flows through a coil (or any wire) it produces a magnetic field in the space outside the wire, and the coil acts just like any natural, permanent magnet, attracting iron and other magnets. If you move a wire through a magnetic field, a current will be generated in the wire and will flow through the associated circuit. It takes energy to move the wire through the field, and that mechanical energy is transformed to electrical energy. This is how an electrical generator works. If the current through a coil is stopped, the magnetic field must also disappear, but it cannot do so immediately. The field represents stored energy and that energy must go somewhere. The field contracts toward the coil, and the effect of the field moving through the wire of the coil is the same as moving a wire through a stationary field: a current is generated in the coil. This induced current acts to keep the current flowing in the coil; the induced current opposes any change, an increase or a decrease, in the current through the inductor. Inductors are used in circuits to smooth the flow of current and prevent any rapid changes.

The current in an inductor is analogous to the voltage across a capacitor. It takes time to change the voltage across a capacitor, and if you try, a large current flows initially. Similarly, it takes time to change the current through an inductor, and if you insist, say by opening a switch, a large voltage will be produced across the inductor as it tries to force current to flow. Such induced voltages can be very large and can damage other circuit components, so it is common to connect some element, like a resistor or even a capacitor across the inductor to provide a current path and absorb the induced voltage. (Often, a diode, which we will discuss later, is used.)

Inductors are measured in henrys (h), another very big unit, so you are more likely to see millihenries, and microhenries. There are almost no inductors on the RoboBoard, but you will be using some indirectly: the motors act like inductors in many ways. In a sense an electric motor is the opposite of an electrical generator. If current flows through a wire that is in a magnetic field (produced either by a permanent magnet or current flowing through a coil), a mechanical force will be generated on the wire. That force can do work. In a motor, the wire that moves through the field and experiences the force is also in the form of a coil of wire, connected mechanically to the shaft of the motor. This coil looks like and acts like an inductor; if you turn off the current (to stop the motor), the coil will still be moving through the magnetic field, and the motor now looks like a generator and can produce a large voltage. The resulting inductive voltage spike can damage components, such as the circuit that controls the motor current. In the past this effect destroyed a lot of motor controller chips and other RoboBoard components. The present board design contains special diodes that will withstand and safely dissipate the induced voltages -- we hope.

Combinations of Inductors

You already know how inductors act in combination because they act just like resistors. Inductance adds in series. This makes physical sense because two coils of wire connected in series just looks like a longer coil. Parallel connection reduces inductance because the current is split between the several coils and the fields in each are thus weaker.

Semiconductor Devices

 

The Truth About Charge   

Our statements above about charge are not wrong, but they are simple and incomplete. In order to understand how semiconductor devices work one needs a more complete description of the nature of charge in the real world. Charge does not exist independently; it is carried by subatomic particles. For this discussion we will be concerned primarily with electrons, which carry a negative charge of $1.6\; �\; 10$^-19 C , the minimum amount of charge that can exist in isolation. At least, no one has found any smaller amount than this fundamental quantum of charge.

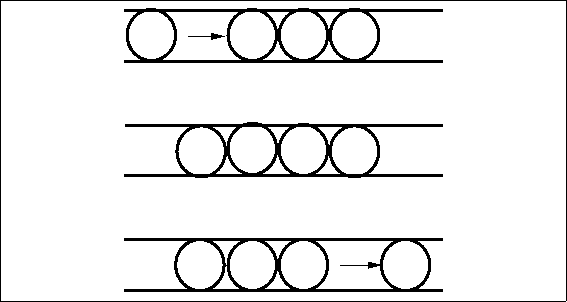
Electrons are one component of atoms and molecules. Atoms are the building blocks out of which all matter is constructed. Atoms bond with each other to form substances. Substances composed of just one type of atom are called elements. For example, copper, gold and silver are all elements; that is, each of them consists of only one type of atom. More complex substances are made up of more than one atom and are known as compounds. Water, which has both hydrogen and oxygen atoms, is such a compound. The smallest unit of a compound is a molecule. A water molecule, for example, contains two hydrogen atoms and one oxygen atom.

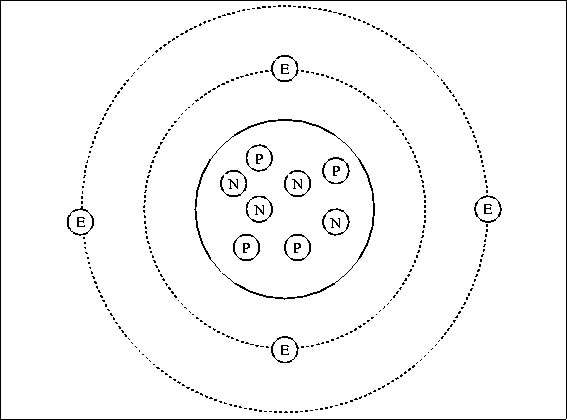
Atoms themselves are made up of even smaller components: protons, neutrons and electrons. Protons and neutrons form the nucleus of an atom, while the electrons orbit the nucleus. Protons carry positive charge and electrons carry negative charge; the magnitude of the charge for both particles is the same, one quantum charge, $1.6\; �10$^-19 C . Neutrons are not charged. Normally, atoms have the same number of protons and electrons and have no net electrical charge.

  

Figure 4.8: Structure of an Atom

Electrons that are far from the nucleus are relatively free to move around under the influence of external fields because the force of attraction from the positive charge in the nucleus is weak at large distances. In fact, it takes little force in many cases to completely remove an outer electron from an atom, leaving an ion with a net positive charge. Once free, electrons can move at speeds approaching the speed of light (roughly 670 million miles per hour) through metals, gases and vacuum. They can also become attached to another atom, forming an ion with net negative charge.

Electric current in metal conductors consists of a flow of free electrons. Because electrons have negative charge, the flow of electrons is in a direction opposite to the positive current. Free electrons traveling through a conductor drift until they hit other electrons attached to atoms. These electrons are then dislodged from their orbits and replaced by the formerly free electrons. The newly freed electrons then start the process anew. At the microscopic level, electron flow through a conductor is not a steady stream, like water flowing from a faucet, but rather a series of short bursts.

  

Figure 4.9: A Simple Model of Electron Flow

Silicon   

 

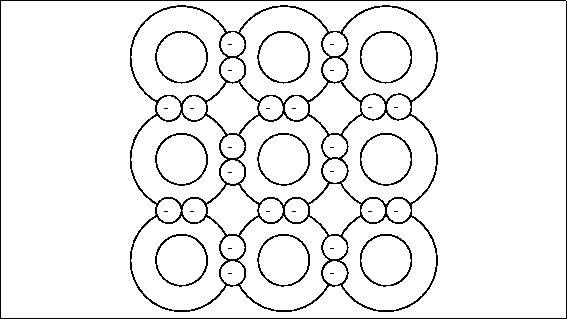
Semiconductor devices are made primarily of silicon (silicon's element symbol is "Si"). Pure silicon forms rigid crystals because of its four valence (outermost) electron structure -- one Si  atom bonds to four other Si atoms forming a very regularly shaped diamond pattern. Figure 4.10 shows part of a silicon crystal structure.

  

Figure 4.10: A Silicon Crystal Structure

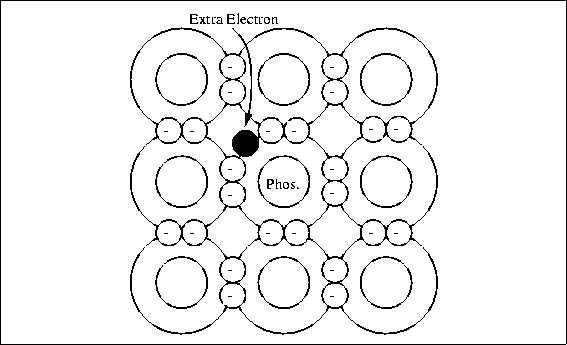
Pure silicon is not a conductor because there are no free electrons; all the electrons are tightly bound to neighboring atoms. To make silicon conducting, producers combine or "dope" pure silicon with very small amounts of other elements like boron or phosphorus. Phosphorus has five outer valence electrons. When three silicon atoms and one phosphorus atom bind together in the basic silicon crystal cell of four atoms, there is an extra electron and a net negative charge. Figure4.11 shows the crystal structure of phosphorus doped silicon.

  

Figure 4.11: Silicon Doped with Phosphorus

This type of material is called n-type silicon. The extra electron in the crystal cell is not strongly attached and can be released by normal thermal energy to carry current; the conductivity depends on the amount of phosphorus added to the silicon.

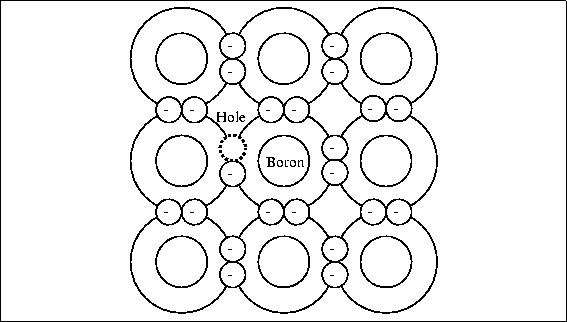
Boron has only three valance electrons. When three silicon atoms and one boron atom bind with each other there is a "hole" where another electron would be if the boron atom were silicon; see Fig. 4.12. This gives the crystal cell a positive net charge (referred to as p-type silicon), and the ability to pick up an electron easily from a neighboring cell.

  

Figure 4.12: Silicon Doped with Boron

The resulting migration of electron vacancies or holes acts like a flow of positive charge through the crystal and can support a current. It is sometimes convenient to refer to this current as a flow of positive holes, but in fact the current is really the result of electrons moving in the opposite direction from vacancy to vacancy.

Diodes   

  

Both p-type and n-type silicon will conduct electricity just like any conductor; however, if a piece of silicon is doped p-type in one section and n-type in an adjacent section, current will flow in only one direction across the junction between the two regions. This device is called a diode and is one of the most basic semiconductor devices.

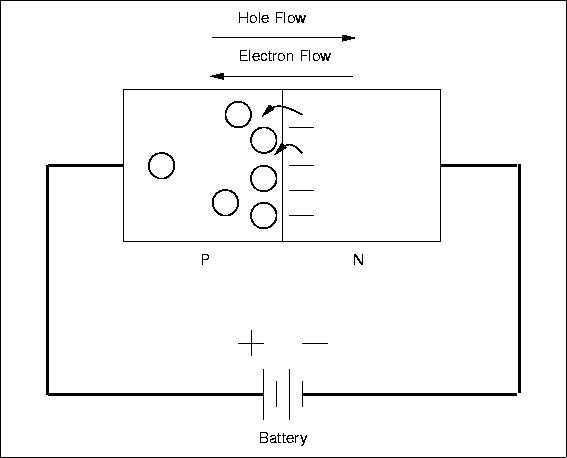
A diode is called forward biased if it has a positive voltage across it from from the p- to n-type material. In this condition, the diode acts rather like a good conductor, and current can flow, as in Fig. 4.13.

  

Figure 4.13: A Forward Biased Diode

There will be a small voltage across the diode, about 0.6 volts for Si, and this voltage will be largely independent of the current, very different from a resistor.

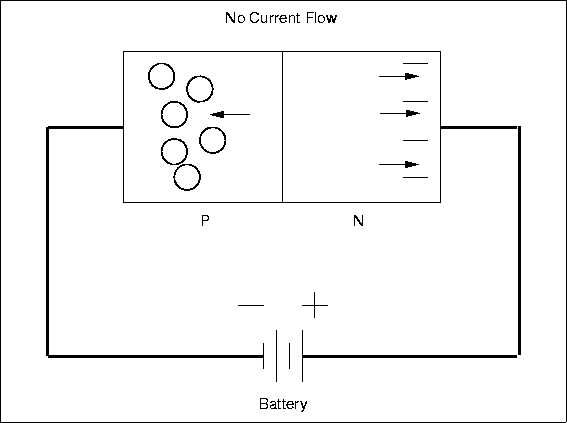
If the polarity of the applied voltage is reversed, then the diode will be reverse biased and will appear nonconducting (Fig. 4.14). Almost no current will flow and there will be a large voltage across the device.

  

Figure 4.14: A Reverse Biased Diode

The non-symmetric behavior is due to the detailed properties of the pn-junction. The diode acts like a one-way valve for current and this is a very useful characteristic. One application is to convert alternating current (AC), which changes polarity periodically, into direct current (DC), which always has the same polarity. Normal household power is AC while batteries provide DC, and converting from AC to DC is called rectification. 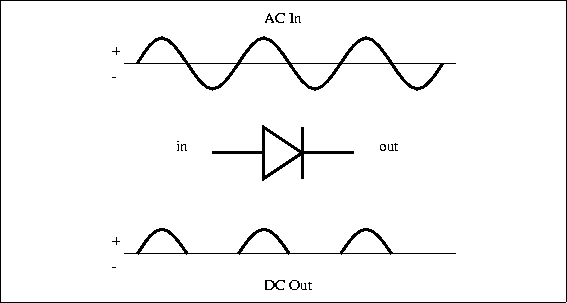Diodes are used so commonly for this purpose that they are sometimes called rectifiers, although there are other types of rectifying devices. Figure 4.15 shows the input and output current for a simple half-wave

  

Figure 4.15: A Half-Wave Rectifier

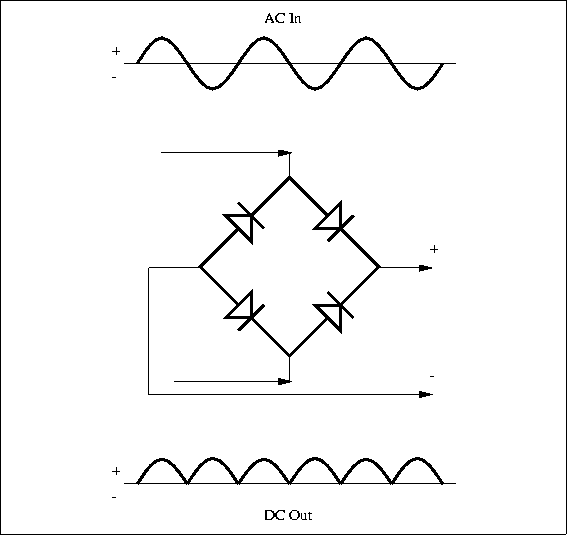
rectifier. The circuits gets its name from the fact that the output is just the positive half of the input waveform. A full-wave rectifier circuit (shown in Figure 4.16) uses four diodes arranged so that both polarities of the input waveform can be used at the output.

  

Figure 4.16: A Full-Wave Rectifier

The full-wave circuit is more efficient than the half-wave one. 

Home / Transistors / FET Current Source

FET Current Source

FET constant current sources use JFETs and MOSFETs to deliver a load current which remains constant despite changes in load resistance or supply voltage

An FET Current Source is a type of active circuit which uses a Field Effect Transistor to supply a constant amount of current to a circuit. But why would you want a constant current? Constant current sources and current sinks, (a current sink is the reverse of a current source) are a very simple way of forming biasing circuits or voltage references with a constant value of current, for example, 100uA, 1mA or 20mA using just a single FET and resistor.

Constant current sources are commonly used in capacitor charging circuits for accurate timing purposes or in rechargeable battery charging applications, as well as linear LED circuits for driving strings of LED’s at a constant brightness.

Resistive voltage references can also be formed using constant current sources, because if you know the value of the resistance and the current flowing through it is constant and steady, then you can simply use Ohm’s law to find the voltage drop.

However, the key to creating an accurate and reliable FET based constant current source depends on using low transconductance FET’s as well as precision resistor values to convert the current into a precise and stable voltage.

Field-effect transistors are commonly used to create a current source with Junction-FET’s (JFET’s) and Metal-oxide Semiconductor MOSFET’s already being used in low current-source applications. In its simplest form, the JFET can be used as a voltage-controlled resistor where a small gate voltage controls the conduction of its channel.

Biasing the Junction FET

We saw in our tutorial about JFET’s that JFET’s are depletion devices and that the N-channel JFET is a “normally-ON” device, until the gate-to-source voltage (VGS) becomes negative enough to turn it “OFF”. The P-channel JFET which is also a “normally-ON” depletion device requires the gate voltage to become positive enough to turn it “OFF”.

N-channel JFET Biasing

 

The image shows the standard arrangement and connections for a common source configured N-channel JFET with normal biasing when used in its active region. Here the gate-source voltage VGS is equal to the gate supply, or input voltage VG which sets the reverse bias between the gate and the source, while VDD provides the drain-to-source voltage and current flow from the supply from drain to source. This current entering the JFET drain terminal is labelled ID.

The drain-source voltage VDS is the JFET’s forward voltage drop and is a function of the drain current, ID for different gate-source values of VGS. When VDS is at its minimum value, the JFET’s conductive channel is fully open and ID is at its maximum value which is called the drain-to-source saturation current ID(sat) or simply IDSS.

When VDS is at its maximum value, the JFET’s conductive channel is fully closed, (pinched-off) so ID reduces to zero with the drain-to-source voltage, VDS being equal to the drain supply voltage VDD. The gate voltage, VGS at which the JFET’s channel stops conducting is referred to as the gate cut-off voltage VGS(off).

This common source biasing arrangement of the N-channel JFET determines the steady state operation of the JFET in the absence of any input signal, VIN as VGS and ID are steady state quantities, that is the quiescent state of the JFET.

Thus for a common-source JFET, the gate-source voltage VGS controls how much current will flow through the JFET’s conductive channel between the drain and source making the JFET a voltage-controlled device because its input voltage controls its channel current. As a result we can develop a set of output characteristic curves by plotting ID versus VGS for any given JFET device.

N-channel JFET Output Characteristic

The JFET as a Constant Current Source

Then we could use this as the n-channel JFET is a normally-ON device and if VGS is sufficiently negative enough, the drain-source conductive channel closes (cut-off) and the drain current reduces to zero. For the n-channel JFET, the closing of the conductive channel between drain and source is caused by the widening of the p-type depletion region around the gate until it completely closes the channel. N-type depletion regions close the channel for a p-channel JFET.

So by setting the gate-source voltage to some pre-determined fixed negative value, we can cause the JFET to conduct current through its channel at a certain value between zero amperes and IDSS respectively making it an ideal FET current source. Consider the circuit below.

JFET Zero-voltage Biasing

 

We saw that the JFET’s output characteristics curves are a plot of ID versus VGS for a constant VDS. But we also noticed that the JFET’s curves do not change very much with large changes in VDS, and this parameter can be very useful in establishing a fixed operating point of the conductive channel.

The simplest constant FET current source is with the JEFT’s gate terminal shorted to its source terminal as shown, the JFET’s conductive channel is open so the flow of current through it will be close to its maximum IDSS value due to the JFET being operated in its saturated current region.

However, the operation and performance of such a constant current configuration is fairly poor as the JFET is constantly in full conduction with the IDSS current value depending completely on device type.

For example, the 2N36xx or the 2N43xx n-channel JFET series is only a few mill-amperes (mA), whereas the larger n-channel J1xx or PN4xxx series can be several ten’s of milli-amperes. Also note that IDSS will vary alot between devices of the same part number as manufacturers quote on their data sheets, minimum and maximum values of this zero gate voltage drain current, IDSS.

Another point to note is that an FET is basically a voltage-controlled resistor whose conductive channel has a resistive value in series with the drain and source terminals. This channel resistance is called RDS. As we have seen, when VGS = 0, maximum drain-to-source current flows, therefore the JFET’s channel resistance, RDS must be at its minimum, and this is true.

However, the channel resistance is not completely zero but at some low ohmic value defined by the manufacturing geometry of the FET and which can be as high as 50 or so Ohms. When an FET is conducting, this channel resistance is commonly known as RDS(ON) and is at its minimum resistive value when VGS = 0. Thus a high RDS(ON) value results in a low IDSS and vice versa.

So a JFET can be biased to operate as an FET current source device at any current value below its saturation current, IDSS when VGS equals zero volts. When VGS is at its VGS(off) cut-off voltage level there will be zero drain current, (ID = 0) as the channel is closed. Thus the channels drain current, ID will always flow as long as the JFET device is operated within its active region as shown.

JFET Transfer Curve

 

Note that for a P-channel JFET, the VGS(off) cut-off voltage will be a positive voltage but its saturation current, IDSS obtained when VGS equals zero volts will be the same as for an N-channel device. Also notice that the transfer curve is nonlinear because the drain current is increasing faster through the opening channel as VGS approaches zero volts.

JFET Negative-voltage Biasing

 

We remember that the JFET is a depletion mode device which is always “ON”, so requires a negative gate voltage for N-channel JFET’s, and a positive gate voltage for P-channel JFET’s to turn them “OFF”. Biasing an N-channel JFET with a positive voltage, or biasing a P-channel JFET with a negative voltage will open the conductive channel even further forcing the channel current, ID beyond IDSS.

But if we use the characteristic curves of ID against VGS, we can set VGS to some negative voltage level, say -1V, -2V or -3V too create a fixed JFET constant current source of whatever current level we require between zero and IDSS.

But for a more accurate constant current source with improved regulation, it is better to bias the JFET at about 10% to 50% of its maximum IDSS value. This also helps with I2*R power losses through the resistive channel and therefore reduced heating effect.

So we can see that by biasing a JFET’s gate terminal with some negative voltage value, or a positive voltage for a P-channel JFET, we can establish its operating point allowing the channel to conduct and pass a certain value of drain current, ID. For different values of VGS, a JFET drain current ID can be expressed mathematically as being:

JFET Drain Current Equation

FET Constant Current Source Example No1

The manufacturers datasheet for a J107 N-channel switching JFET shows that it has an IDSS of 40mA when VGS = 0, and a maximum VGS(off) value of -6.0 volts. Using these declared values, calculate the JFET’s drain current value when, VGS = 0, VGS = -2 volts, and when VGS = -5 volts. Also show the J107’s transfer characteristic curve.

1). When VGS = 0V

When VGS = 0V the conductive channel is open and maximum drain current flows.

Thus ID = IDSS = 40mA.

 

2). When VGS = -2V

 

3). When VGS = -5V

 

4). J107 Transfer Characteristic Curve

 

Thus we can see that as the gate-source voltage, VGS approaches the gate-source cut-off voltage, VGS(off) the drain current, ID decreases. In this simple example, we calculated the drain current at two points, but calculating using additional values of VGS between zero and cut-off would give us a more accurate shape of the curve.

JFET Current Source

A JFET can be made to operate as a voltage controlled constant current source whenever its gate-source junction is reverse biased, and for an N-channel device we need a -VGS and for a P-channel device we need a +VGS. The problem here is that the JFET requires two separate voltage supplies, one for VDD and another for VGS.

However if we place a resistor between the source and ground (0 volts), we can achieve the necessary VGS self-biasing arrangement for the JFET to operate as a constant current source using only the VDD supply voltage. Consider the circuit below.

JFET Current Source

At first glance you may think that this configuration looks very similar to a JFET common drain (source follower) circuit we saw in the JFET tutorial.

However the difference this time is that while the FET’s gate terminal is still tied directly to ground (VG = 0), the source terminal is at some voltage level above zero voltage ground due to the voltage drop across the source resistor, RS.

Therefore, with a channel current flowing through the external source resistor, the gate-to-source voltage of the JFET will be less than (more negative than) zero (VGS < 0).

The external source resistor, RS provides a feedback voltage which is used to self-bias the JFET’s gate terminal keeping the drain current constant through the channel despite any changes in the drain-source voltage. Thus the only voltage source we need is the supply voltage VDD to provide the drain current and bias.

So the JFET uses the voltage drop across source resistor (VRS) to set the gate bias voltage VGS and therefore the channel current as we have seen above. Thus, increasing the resistive value of RS will decrease the channels drain current ID, and vice versa. But if we wanted to construct a JFET constant current source circuit, what would be a suitable value for this external source resistor, RS.

Manufacturers data sheets for a particular N-channel JFET will give us the values of VGS(off) and IDSS. Knowing the values of these to two parameters we can transpose the above JFET equation for the drain current, ID to find the value of VGS for any given value of drain current, ID between zero and IDSS as shown.

JFET Gate to Source Voltage Equation

 

Having found the gate-to-source voltage required for a given drain current, the value of the source biasing resitor value required is found by simply using Ohm’s law, as R = V/I. Thus:

JFET Source Resistor Equation

FET Constant Current Source Example No2

Using the J107 N-channel JFET device from above which has an IDSS of 40mA when VGS = 0, and a maximum VGS(off) value of -6.0 volts. Calculate the value of the external source resistor required to produce a constant channel current of 20mA and again for constant current of 5mA.

1). VGS for ID = 20mA

 

2). VGS for ID = 5mA

 

Thus when VGS(off) and IDSS are both known, we can use the above equations to find the source resistance required to bias the gate voltage for a particular drain current, and in our simple example this was 87.5Ω at 20mA, and 776Ω at 5mA. So the addition of an external source resistor allows for the adjustment of the current source output.

If we was to replace the fixed value resistors with a potentiometer we can make the JFET constant current source fully adjustable. For example, we could replace the two source resistors in the above example with one 1kΩ potentiometer, or trimmer. Also as well as being fully adjustable, this JFET constant current source circuits drain current will remain constant even with changes in VDS.

FET Constant Current Source Example No3

An N-channel JFET is required to vary the brightness of a 5mm round red LED load between 8mA and 15mA. If the JFET constant current source circuit is fed from a 15 volt DC supply, calculate the JFET’s source resistance required to illuminated the LED between minumum and maximum brightness when the switching JFET has a maximum VGS(off) value of -4.0 volts and an IDSS of 20mA when VGS = 0. Draw the circuit diagram.

1). VGS for ID = 8mA

 

2). VGS for ID = 15mA

 

Then we would need an external potentiometer capable of varying its resistance between 36Ω and 184Ω. The nearest preferred potentiometer value would be 200Ω.

Adjustable JFET Constant Current Source

 

A potentiometer or trimmer used instead of a fixed value source resistance, RS would allow us to vary or fine-tune the current flowing through JFET’s conductive channel.

However, in order to ensure a good current regulation through the FET device, and therefore a more stable current flow, it would be better to limit the maximum channel current flowing through the LED (15mA in this example) to between 10% and 50% of the JFETs IDSS value.

Creating constant current sources using MOSFET’s allows for much greater channel currents and better current regulation, and unlike JFET’s which are only available as normally-on depeletion mode devices, MOSFET’s are available in both depletion-mode (normally-on) and enhancement-mode (normally-off) devices as either P-channel or N-channel types allowing for a greater range of current source options.

FET Constant Current Source Summary

We have seen in this tutorial about the FET Constant Current Source that due to their channel resistance characteristics, field effect transistors can be used to supply a constant current to a load and find numerous applications in electronics circuits where it is required to supply a fixed current to a connected load.

Constant current circuits can be built using depletion mode FET’s but also using BJT’s (bipolar junction transistors), or a combination of these two devices. Remembering that the JFET is a voltage-controlled device, not a current-controlled device like the bipolar junction transistor.

One of the main characteristics of a Junction Field Effect Transistor, or JFET, is that because it is a depeltion device, its conductive channel is always open so it requires a gate-to-source voltage, VGS to turn it “OFF”.

The VGS(off) voltage required for an N-channel JFET ranges from 0 volts, for full conduction of the channel, to some negative value, usually several volts, required to turn the JFET fully-OFF, thus closing the channel. So by biasing the JFET’s gate terminal at some fixed value between zero and VGS(off), we can control the channels depletion layers width and therefore its resistive value, passing a fixed and constant amount of current. For a P-channel JFET, its VGS(off) value ranges from 0 volt for full channel conduction to some positive value of several volts for a particular VDS value.

The regulation and tolerance of the constant current for a given JFET device is related to the amount of drain current, ID passing through the channel. The lower the drain current through a particular devive, the better the regulation. Biasing a JFET at between about 10% to 50% of its maximum IDSS value will improve the devices regulation and performance. This is achieved by connected an external resististance between the source and gate terminals.